Die Wasserdampfdiffusions-Widerstandszahl (µ-Wert) eines Materials gibt an, um wieviel größer der Diffusionswiderstand des Materials im Vergleich zu ruhender Luft ist. Der µ-Wert einer Materialprobe kann ermittelt werden, indem man die Probe auf beiden Seiten verschiedenen relativen Luftfeuchten aussetzt und den resultierenden Diffusionsstrom durch die Probe misst. Ist die Probe eine dünne Materialschicht, etwa eine Folie, dann kann sie zur Messung über die Öffnung einer Schüssel („Cup“) gespannt werden. Die gewünschte relative Feuchte kann in der Schüssel mit einem Trocknungsmittel oder einer geeigneten Salzlösung eingestellt werden, während außerhalb der Schüssel z.B. eine Klimakammer die gewünschte Feuchte konstant hält.
Während der Messung herrschen entlang des Materialquerschnitts verschiedene Feuchten. Sie variieren von der Feuchte, die an der einen Oberfläche anliegt, bis zur Feuchte an der anderen Oberfläche. Bei Materialien mit feuchteabhängigem µ-Wert, wie etwa bei feuchteadaptiven Dampfbremsen, entsprechen diese verschiedenen Feuchten verschiedenen µ-Werten. Der Dampfstrom trifft auf seinem Weg durch den Probenquerschnitt auf diese Abfolge verschiedener µ-Werte. Die Stärke des resultierenden Dampfstroms lässt auf den Gesamtwiderstand der Probe in diesem Feuchtezustand schließen, aber nicht unmittelbar auf die beteiligten Einzelwiderstände bei den individuellen Feuchten an verschiedenen Stellen der Probe.
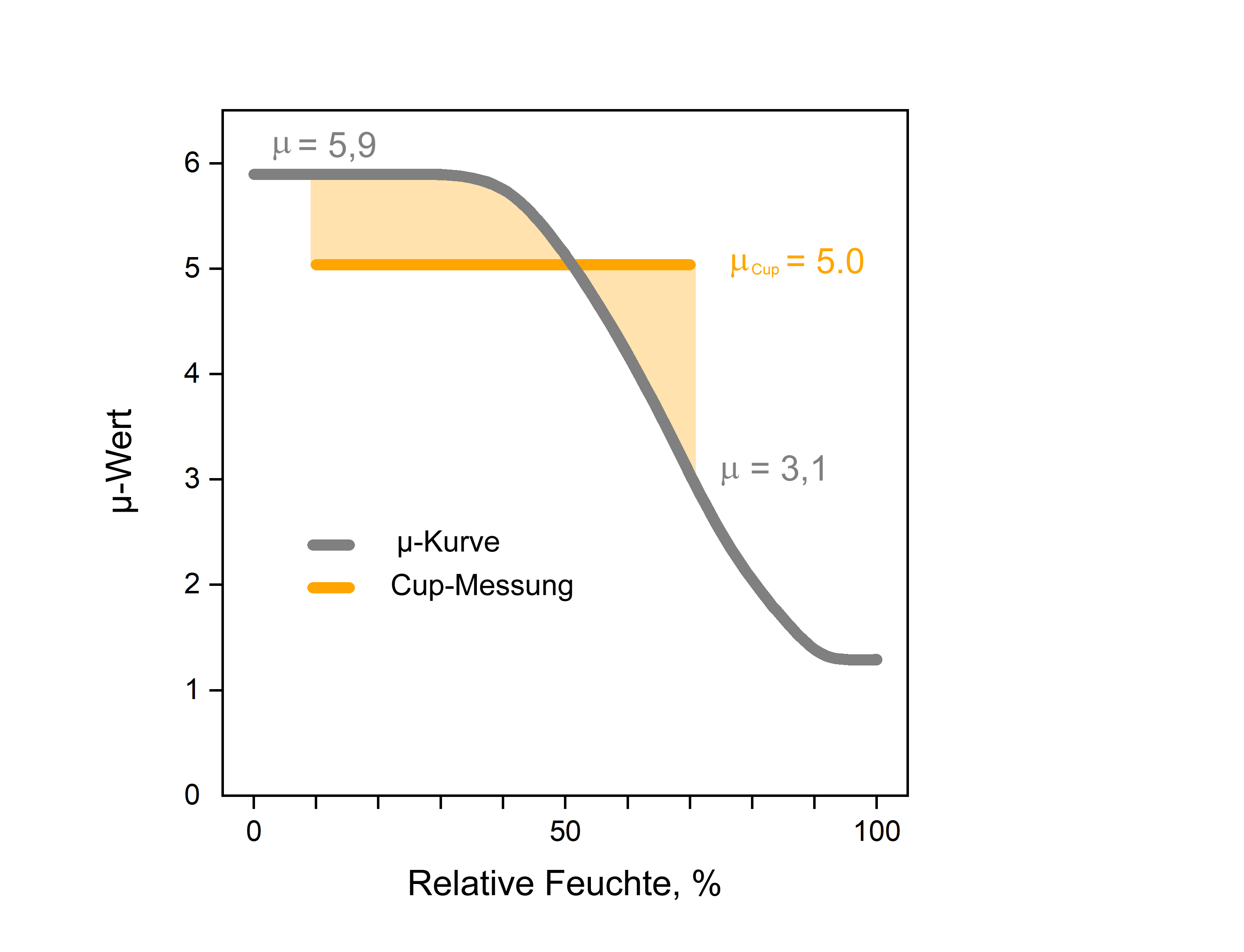
Der Gesamtwiderstand µCup der Probe ist der Mittelwert (genauer: das „harmonische Mittel“) der µ-Kurve im angelegten Feuchtebereich. Im folgenden Beispiel liegen an den Probenoberflächen die relativen Feuchten 10 % und 70 % an, was bei diesem Material den µ-Werten 5,9 und 3,1 entspricht. Der Gesamtwiderstand ergibt sich als Mittelwert der dazwischen liegenden Kurve und beträgt hier µCup = 5,0:
Dies ist eine Aussage über das mittlere Widerstandsniveau in dem bei dieser Messung angelegten Feuchtebereich. In der Regel soll jedoch der punktweise Verlauf der µ-Kurve des Materials möglichst detailliert ermittelt werden. Außerdem kann die Kurve für den gesamten Feuchtebereich von 0 % bis 100 % verlangt sein. Diese Forderungen können durch Kombination von Cup-Messungen mit verschiedenen Feuchtebereichen erfüllt werden.
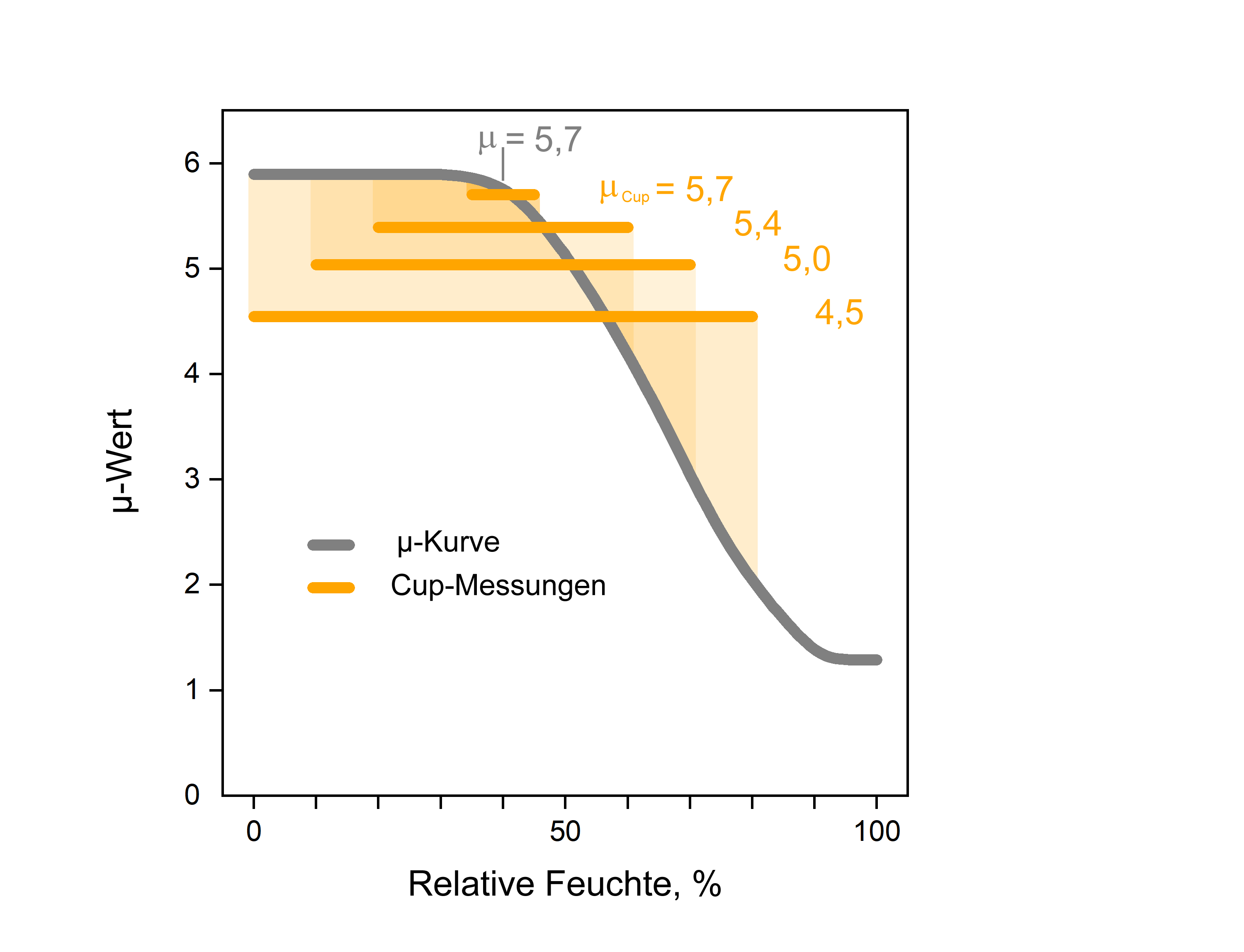
Es wird oft angenommen, dass sich die einzelnen Punkte der µ-Kurve ergeben, wenn die aus den Cup-Messungen folgenden Gesamtwiderstände gegen die mittlere jeweils angelegte Feuchte aufgetragen werden. Bei stark nicht-linearen Kurven ist dies jedoch nicht zutreffend, wie das folgende Beispiel zeigt. Cup-Messungen, bei denen Feuchtebereiche mit demselben Mittelwert (hier 40 %) aber zunehmender Breite angelegt sind, ergeben abnehmende Gesamtwiderstände, weil mit breiter werdendem Feuchtebereich auf der rechten Seite immer größere Teile des abnehmenden Kurvenbereichs in den gemessenen Feuchtebereich gelangen, während der konstante Kurvenbereich auf der linken Seite stets denselben Beitrag zum Mittelwert liefert.
In diesem Beispiel liefert ein Cup-Versuch mit den angelegten Feuchten 35 % und 45 % einen Gesamtwiderstand µCup von 5.7 und damit praktisch den Kurvenwert für 40 %, während eine Messung mit angelegten 0 % und 80 % Feuchten bei gleicher mittlerer Feuchte nur einen Gesamtwiderstand µCup = 4.5 ergibt.
Der aus einer Cup-Messung folgende Gesamtwiderstand µCup ist also in der Regel nicht identisch mit dem individuellen µ-Wert bei der mittleren Messfeuchte, die Größe der Abweichung hängt darüber hinaus auch von der Breite des angelegten Feuchtebereiches ab.
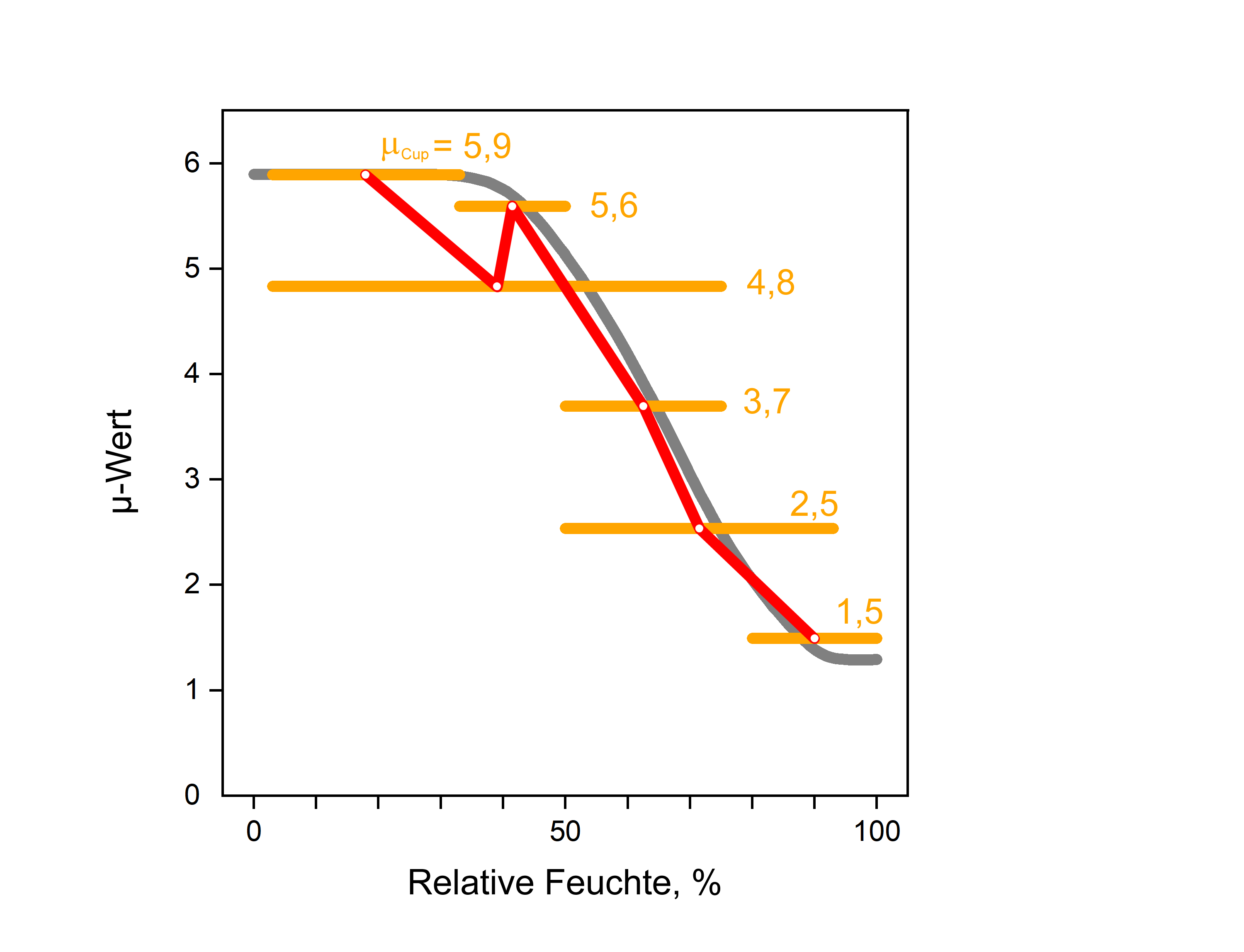
Das folgende Bild zeigt als rote Kurve einen irreführenden Verlauf einer µ-Kurve, wie er sich beispielhaft bei unkritischer Auftragung der jeweiligen Cup-Messung gegen die mittlere Feuchte ergeben könnte:
Neben der teilweise irreführenden Kurvenform ist die rote Kurve im Allgemeinen auch nicht zahlenmäßig mit der Originalkurve deckungsgleich, so dass es mit der roten Kurve insbesondere nicht einmal möglich wäre, die ihr zugrunde liegenden Cup-Messungen in einer hygrothermischen Simulationsrechnung nachzuvollziehen. Bei modernen, stark feuchtevariablen Folien kann die Abweichung zwischen den mit falscher µ-Kurve durchgeführten Simulationen und den Originalmessungen unter Umständen einen Faktor zwei bis drei ausmachen.
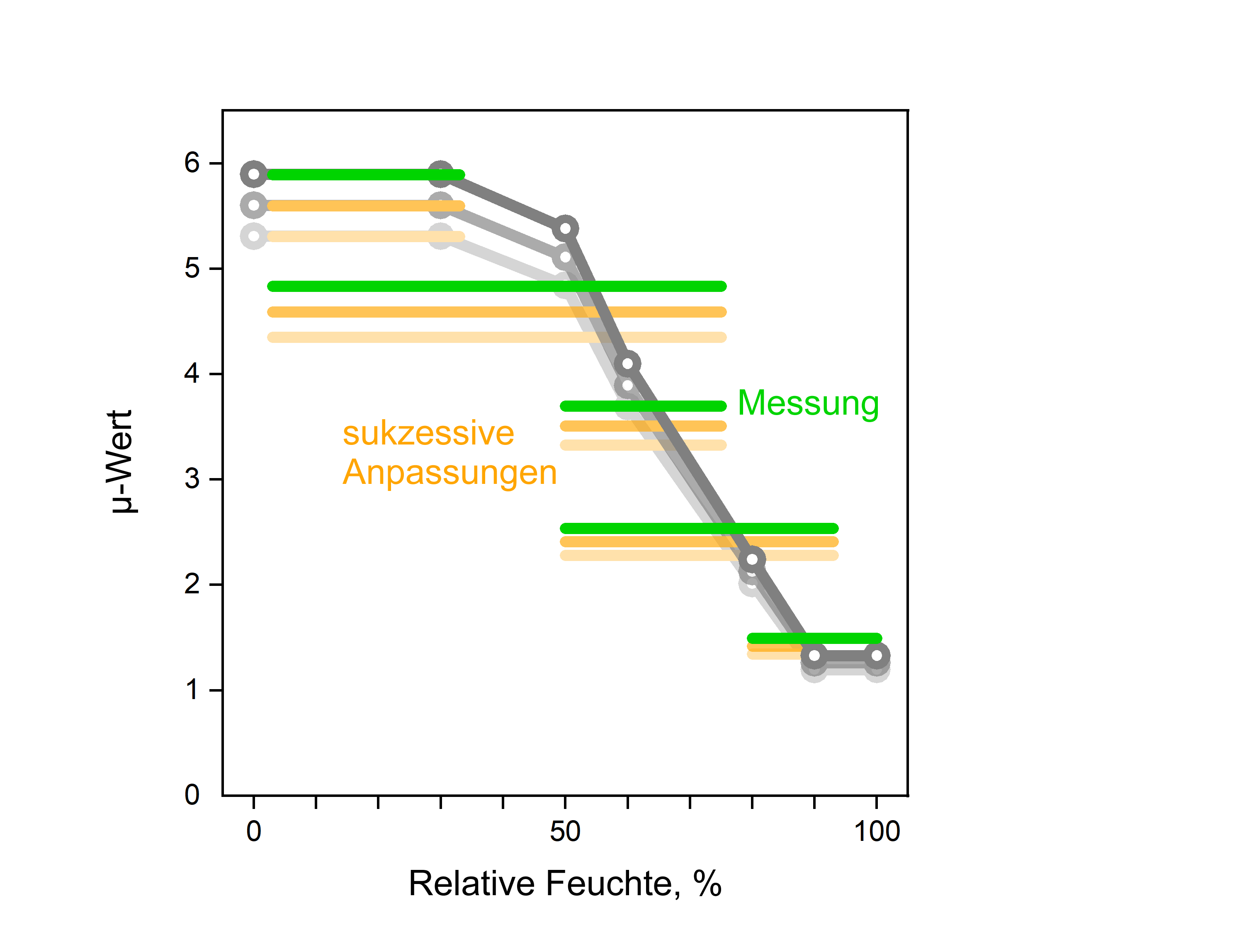
Die Aufgabe besteht daher darin, eine Kurve so zu erstellen, dass die Mittelwerte bestimmter Kurvenbereiche vorgegebene Werte annehmen. Eine Möglichkeit ist es, eine durch einen Polygonzug dargestellte Testkurve so lange anzupassen, bis alle gesuchten Mittelwerte möglichst gut erreicht werden. Aufgrund experimenteller Unsicherheiten bei den Cup-Messungen ist es meistens nicht möglich, perfekte Übereinstimmung mit allen Mittelwerten zu erreichen. In diesem Fall wird die beste Übereinstimmung im Sinne kleinster Fehlerquadrate ermittelt.
Je mehr Feuchtebereiche für die Auswertung zur Verfügung stehen, um so detaillierter und zuverlässiger kann der Verlauf der µ-Kurve ermittelt werden. Anfang und Ende der ermittelten Kurve sind mit geringerer Sicherheit bestimmt. Um unsichere Extrapolationen zu vermeiden, bietet es sich an, das erste und letzte Segment des Polygonzugs als konstant vorauszusetzen.
Anzahl und Lage der Kurvenstützstellen können so gewählt werden, dass sie den Kurvenverlauf auf der gegebenen Datengrundlage bestmöglich abbilden. Die ermittelten Stützpunkte der resultierenden Kurve können direkt für deren Tabellierung (z.B. in WUFI) verwendet werden.
Zuletzt geändert: